例题1

粗糙水平地面上放置一质量为m的木块，木块与地面的摩擦因数为μ，一个人想把木块匀速拉走，请问该人至少要对木块施加多大的力。

解答1

令拉力F与水平面夹角为$\alpha$，简单受力分析可得

$$
\begin{cases}
F \cdot{cos \alpha}=f \\
N+F \cdot{sin \alpha}=G
\end{cases}
$$

联立上述式子，解得

$$
F(cos \alpha+μsin \alpha)=μmg
$$

对于这个式子，可用数学上对同角三角函数的常用处理方法，对其进行化简。
由其系数得

$$
k=\sqrt{1+μ^2}
$$

原式提取出k，则原式可以转化为

$$
\sqrt{1+μ^2}F(\frac{1}{\sqrt{1+μ^2}}cos \alpha+\frac{μ}{\sqrt{1+μ^2}}sin \alpha)=μmg
$$

令

$$
sin\theta=\frac{1}{\sqrt{1+μ^2}}
$$

则

$$
cos\theta=\frac{μ}{\sqrt{1+μ^2}}
$$

原式化为

$$
\begin{align}
\sqrt{1+μ^2}F(sin\theta cos \alpha+cos\theta sin \alpha)=μmg \\
Fsin(\theta + \alpha)=\frac{μmg}{\sqrt{1+μ^2}}
\end{align}
$$

对于$Fsin(\alpha + \theta)$，当$\alpha+\theta=\frac{\pi}{2}$时$sin$取得最大值，即原题答案为

$$
当\alpha+\theta=\frac{\pi}{2}时 \\
F最小，F_{min}=\frac{μmg}{sin(\theta + \alpha)\sqrt{1+μ^2}}
$$

例题2

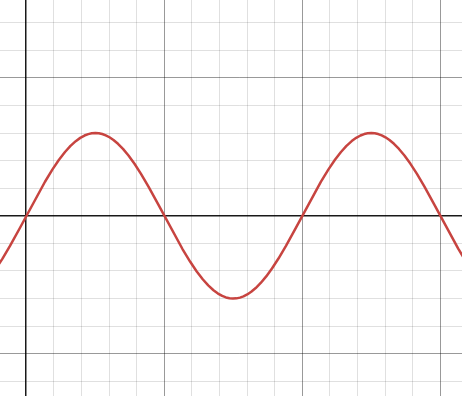
已知质量为m的物体在劲度系数为k的弹簧作用下水平方向作简谐运动， 振子相对平衡位置的位移与时间的关系如下图所示，求振动的速度和加速度。

解答2

根据其图像可知，振动方程为

$$
x=Asin\frac{2\pi}{T}t
$$

其中A为振幅，则速度和加速度分别为

$$
v=\frac{dx}{dt}=\frac{d(Asin\frac{2\pi}{T}t)}{dt}=A\omega cos\frac{2\pi}{T}t
$$

由上式可知，如果位移按照正弦规律变化，则速度按照余弦规律变化，当速度最大时位移为0，速度为0时位移最大。

$$
a=\frac{d v}{d t}=\frac{d\left(A \frac{2 \pi}{T} \cos \frac{2 \pi}{T} t\right)}{d t}=-A\left(\frac{2 \pi}{T}\right)^{2} \sin \frac{2 \pi}{T} t=-\left(\frac{2 \pi}{T}\right)^{2} x
$$

由上式可知。加速度与位移成正比且反向